BDA-602 - Machine Learning Engineering
Dr. Julien Pierret
Lecture 9
The Case Against Machine Learning
-
Minimum Viable Product (MVP)
- Just enough features to deploy the product
-
Deploy to a subset of "nice" early adopters
- Forgiving
- Give feedback
- Machine learning may be more than the minimum
-
Building models
- Time
- Data
-
Simple programatic solutions are better
- Come to life faster
-
Cheaper to produce
- Don't need tons of data
- Don't need compute
›
Avoidance is not Prevention
- Start with a programming solution
-
Get everything working
- Frontend
- Backend
-
Move to a simple model
- Don't jump to Deep Learning
-
Other problems need to be solved first
- Deployment?
- Getting data?
- Updating data?
- Training the model?
- Iterate,...
- Iterate,...
- Iterate,...
›
Planet Labs 🛰️
-
Saw a presentation on how they operate
- Continuous Integration for hardware
- They are simply amazing
- Commissioning the World's Largest Satellite Constellation
›
Story-time - Maintenance Chatbot 🤖
- Please ask questions as I go along
›
Higher Dimensional Optimizations
-
Example shown was solving 1 dimensional problems
- With the help of the Hessian matrix we can do this in higher dimensional space
- Number of dimensions get really big, Hessian too computationally expensive
- Newton is just one technique
-
Extremely important topic
- SDSU class - Math 693a - Excellent class
-
Why does this matter?
- Models are all doing this!
›
Optimization Problems
-
Mathematical Optimizations
- Many fields
- Can't always build an optimization function
-
NPV Optimization Problem:

-
Employee Workflow Optimization Problem:

›
Optimization Problems
-
Excel Solver

- Solution isn't always modeling
-
May already have a function that explains relationship
- Need to maximize/minimize the output of this function
- Subject to some constraints
›
Optimization Problems - Example
- Assume we have a function that takes in 3 inputs
- Subject to a bunch of constraints
$$ f(x, y, z) $$
$$ x < y, x+y > z $$

Optimization Problems - Brute Force
-
We could brute force it
- $x$:
[0, 10] - $y$:
[-10, 10] - $z$:
[20, 10] - We would skip ($x$, $y$, $z$) that are not within our constraints
- Step size important!
- $x$:
-
Problems
-
$f(x,y,z)$ could be expensive
: slow -
Large step size
: miss global max/min -
Small step sizes
: slow
-
$f(x,y,z)$ could be expensive
›
Optimization Problems - Libraries
›
Optimization Problems - Why?
-
These kinds of problems do come up
-
Net Present Value (NPV) calculations
- Minimizing a loss
- Maximizing a profit
-
Net Present Value (NPV) calculations
-
Flexibility
- Modeling not always the solution
- It all depends on the problem you need to solve
- ... now lets build some models!
›
Explainable Models
-
What does it mean to be explainable?
-
You can understand why the model choose what it did
- Coefficients relationship with the variables
-
You can understand why the model choose what it did
- Explainable Models
›
Linear Regression
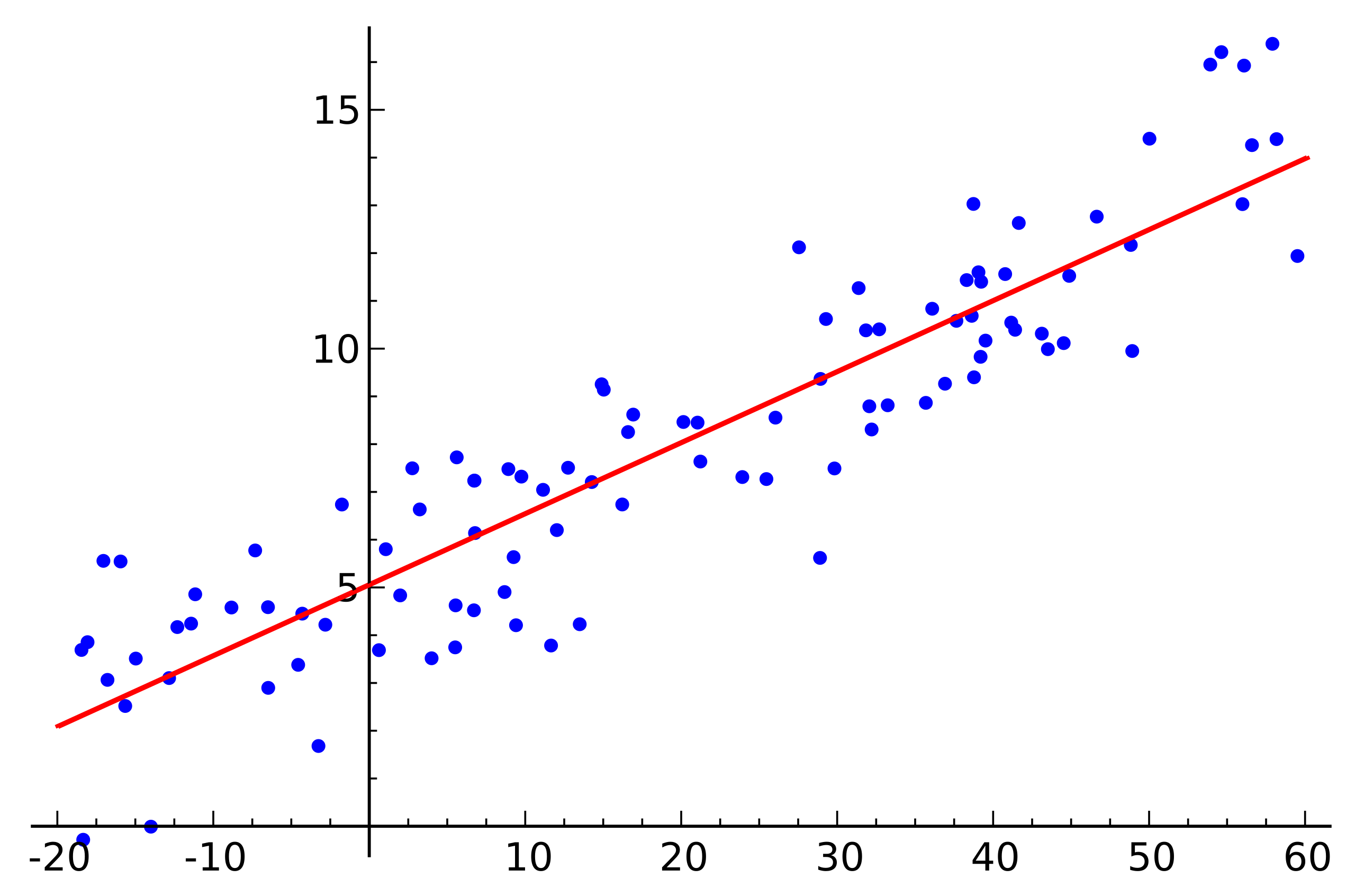
›
Linear Regression
-
sklearn.linear_model.LinearRegression
-
Assumptions
- Linear relationship
- Homoscedasticity
- Normally distributed predictors
- Independence of residuals (errors)
-
No perfect
Multicollinearity
(Rank deficient matrix) - Multicollinearity = BAD
- Why we spent so much time on correlation
›
Logistic Regression
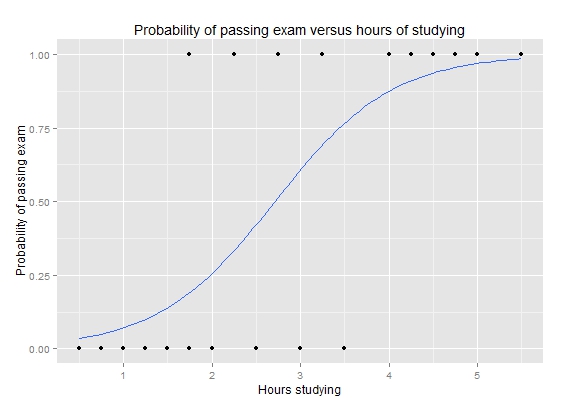
›
Logistic Regression
-
sklearn.linear_model.LogisticRegression
-
Assumptions
- Binary response
- Logit relationship
- Independence of residuals (errors)
-
Little or no
Multicollinearity
(Stricter than linear) - Remember this Multicollinearity problem!
›
Bias-Variance Tradeoff
-
Bias error
- Errors from assumptions in learning algorithm
- High bias and we miss relationships between predictors and response
- Underfitting
-
Variance
- Sensetivity to small fluctuations in training set
- High variance and we model random noise
- Overfitting
- Need to the right balance between them
›
Cross Validation
- Train / Test splits
-
Holdout
- Train on a portion of the dataset -
"Expensive" model to generate
- Neural Networks
- 🐢
- Example: Hold out recent data, train on older data
-
sklearn.model_selection.train_test_split
-
"Expensive" model to generate
-
K-Fold
-
"Cheap" model to generate
- Regression
- Decision Trees
- 🏎️
-
sklearn.model_selection.KFold
-
"Cheap" model to generate
›
Cross Validation - K-fold
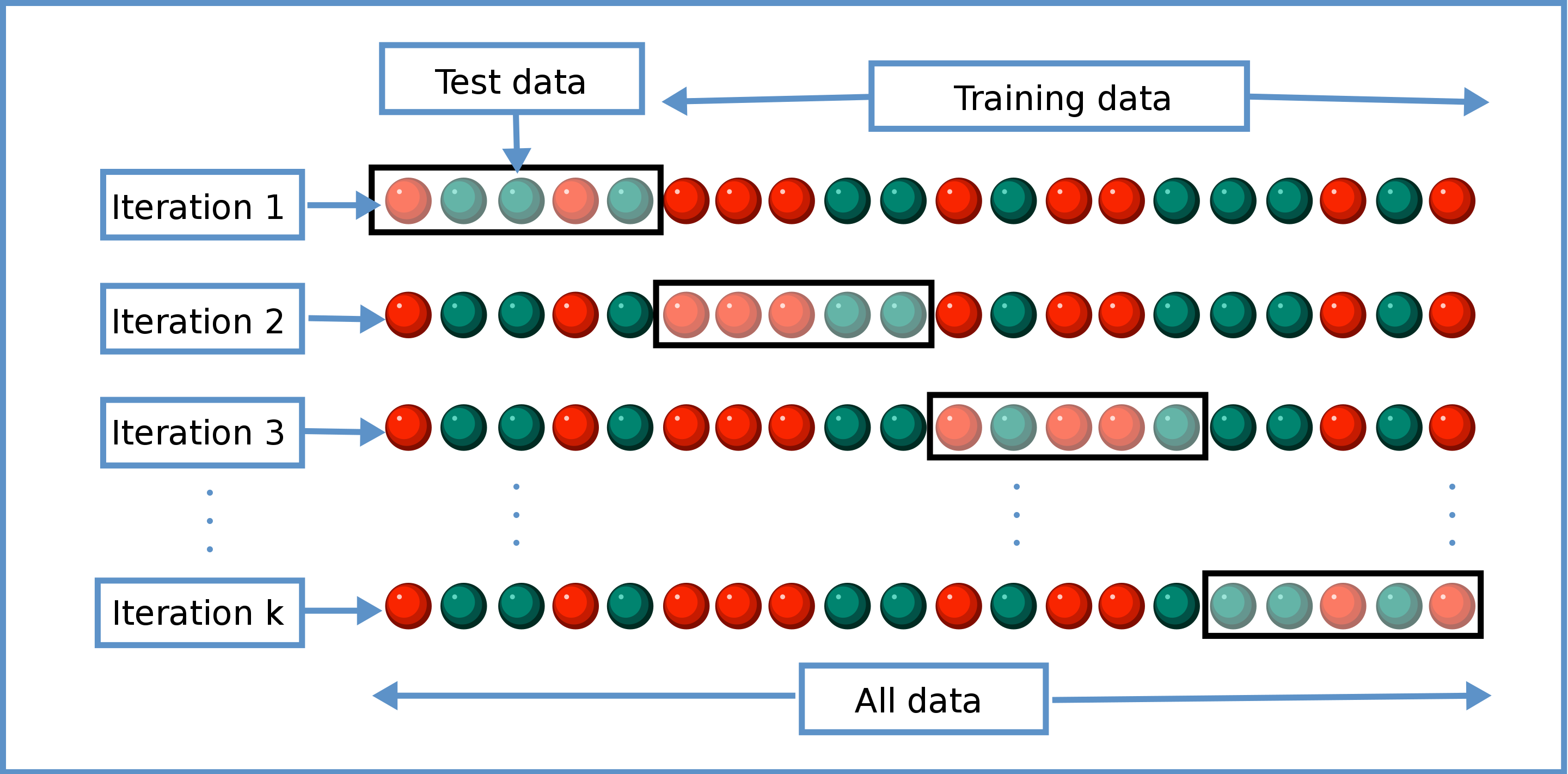
Cross Validation - Stratified
-
Large imbalance in the distribution of the response labels
-
i.e: More
0s than1s - Make sure train/test splits have equal proportion
-
i.e: More
- Holdout
- K-Fold
›
Cross Validation - Grid Search
- sklearn.model_selection.GridSearchCV
- Scoring functions
- Always maximizing the score
›
Cross Validation - Custom
-
Don't like the available scoring functions?
- Make your own
›
Explainable Models - Overfitting
-
Focus
- Regression
- Logistic Regression
-
Variable Selection is very important
- Make or break your model
›
Explainable Models - Features
- You can't use all the features
- Garbage features look like they improve performance
- Let's look at some generated data
›
Explainable Models - Simple Model - Actual vs Predicted
›
Explainable Models - Simple Model - Summary Statistics
›
Explainable Models - Adding Junk
- Picked the correct variables
- What if we pick bad variables?
- Add random garbage!
›
Explainable Models - Adding More Junk
›
Explainable Models - Adding Even More Junk
- Rank Deficent
›
Explainable Models - $R^2$
›
Explainable Models - Overfitting - Predicted vs Actual
›
Explainable Models - Overfitting - MSE
›
Building Explainable Models - Overview
-
Regression Models
- Feature Inspection
- Baseline Model
-
Feature Engineering
- Imagination
-
Brute Force
- Variable Combinations
- Fork Models?
- Feature Selection
-
K-Fold Cross Validation
-
Combinatorics
${n \choose k}$
Feature Selection
- Pick best variable combination for each ${n \choose k}$
- Speeding up the model selection
-
Combinatorics
${n \choose k}$
Feature Selection
›
Building Explainable Models - Feature Inspection
-
Continuous
- Plots
- Rank Ordering
-
Normality assumptions
- Boxcox
-
Categorical
- Plots
- Rank Ordering
-
Sub-categories predictive
- t-test
- ANOVA
- Get a feel for the data
›
Building Explainable Models - Baseline Model
-
Random Forest
- Quick
- Easy
- Performs well
-
Minimal
hyper-parameter tunning
- Don't tune it
›
Building Explainable Models - Feature Engineering
-
Imagination
- How to combine features
- Ways to combine information
- New data sources
- ...
-
Un-supervised Learning
- Try some
- Inspect how they perform
-
Categoricals
- Look-up tables
-
Sub-categories
- Forking models
-
Brute Force
- Inspect the plots, look for patterns
- Come up with new features
›
Building Explainable Models - Feature Selection
-
Correlations
- Continuous / Nominal / Ordinal
- Reduce the number of features
-
Rankings
-
Ignore features with low rankings
- Many ranking techniques
-
Ignore features with low rankings
-
Stepwise regression
- Forwards / Backwards
- Use it to help get the numbers down a bit more
- Not perfect, but may help
›
Building Explainable Models - K-Fold Cross Validation
- Cross Validation Time
- Imagine our final variables are: A, B, C, D
| Choose | # of Combinations | Combinations | Best Avg. MSE |
|---|---|---|---|
| ${4 \choose 1}$ | 4 | {A}, {B}, {C}, {D} | 5 |
| ${4 \choose 2}$ | 6 | {A, B}, {B, C}, {C, D}, {A, C}, {A, D}, {B, D} | 4 |
| ${4 \choose 3}$ | 4 | {A, B, C}, {B, C, D}, {A, C, D}, {A, B, D} | 3 |
| ${n \choose 4}$ | 1 | {A, B, C, D} | 4 |
-
For each ${n \choose k}$
- Pick the best variable combination that minimized avgerage MSE among k-folds
- Not restricted to MSE
›
Building Explainable Models - Too many combinations
| Choose | # of Combinations |
|---|---|
| ${20 \choose 1}$ | 20 |
| ${20 \choose 2}$ | 190 |
| ${20 \choose 3}$ | 1,140 |
| ${20 \choose 4}$ | 4,845 |
| ${20 \choose 5}$ | 15,504 |
| ${20 \choose 6}$ | 38,760 |
| ${20 \choose 7}$ | 77,520 |
| ${20 \choose 8}$ | 125,970 |
| ${20 \choose 9}$ | 167,960 |
| ${20 \choose 10}$ | 184,756 |
| ${20 \choose 11}$ | 167,960 |
| ${20 \choose 12}$ | 125,970 |
| ${20 \choose 13}$ | 77,520 |
| ${20 \choose 14}$ | 38,760 |
| ${20 \choose 15}$ | 15,504 |
| ${20 \choose 16}$ | 4,845 |
| ${20 \choose 17}$ | 1,140 |
| ${20 \choose 18}$ | 190 |
| ${20 \choose 19}$ | 20 |
| ${20 \choose 20}$ | 1 |
Building Explainable Models - Noticing a pattern
- y-axis: Best MSE among the combinatiotns
- X-axis: $k$ in ${n \choose k}$
Building Explainable Models - Polynomial Curve fitting
-
Run calculations on
- $k = 1,2,3,4$
- $k = n, n-1, n-2, n-3$
-
Fit a polynomial to the curve
- Predict which $k$ is the minimum
- Run that $k$
- Repeat
-
If $k$ predicted is $k$ calculated
- Check neighboring $k$'s ($k-1$, $k+1$) to double check
›
Building Explainable Models - Finalizing Model
-
Might be able to improve the model
- Calculate the rankings on the model residuals against all the predictors not used
- Plot everything
- There may be a new variable that works well with the particular variable combination we have
-
Put floors and ceilings on all your continuous predictors
- In production, a wildly small/big number won't disrupt the model
- 1%-5%
-
One final Step
- Those predictors are the best set of variables
- Train final model on the whole dataset with them (no hold-out)
- This is the final model
›
In Summary
- Don't be in a big rush to build models
-
Machine learning background
- Everything is an optimization problem
- Newton's Method
-
Optimization Problems
- Predictive models not always the solution
-
Explainable Models
- Regression based models
-
Cross Validation
- Bias-Variance Tradeoff
- K-Fold, Stratified, Grid Search
- Overfitting
-
Building Explainable models
- Feature Inspection, Engineering, Selection
- Cross-Validation Combinatorics